WordPressで数式を書きたい!
論文とまではいかなくても、何かしら数式が登場する記事を書きたい方はいっぱいいらっしゃるはずです。実際、有名なブログサイトのnoteやQiitaなどでは、数式のサポートがされています。
数式はこんな感じ。インライン記法だと、このように文中に分数 \(\frac{3}{4}\) を記入できたりします。分数の大きさも変えられます。大きい分数 \({\Large\frac{3}{4}}\) 。2次方程式の解の公式は \(x = \frac{-b \pm \sqrt{b^2 – 4ac}}{2a}\) です。
数式行の記法はこんな感じです。
$$x = \frac{-b \pm \sqrt{b^2 – 4ac}}{2a}$$
\[\sin^2 \theta + \cos^2 \theta = 1\]
ということで、WordPressにLaTeX記法を導入する方法をメモ。
MathJax
まずはMathJaxというJavaScriptライブラリ。WebサイトでLaTeX数式が表示されている場合、そのほとんどがMathJaxというライブラリで実現しています。有名サイトだと、Qiitaなど。
プラグインで導入
MathJax-LaTeXというWordPressプラグインで簡単導入できます。
これを投入した後、
[mathjax]というショートコードに続けて数式を書くだけ。こんな感じ
[mathjax]
$$\begin{pmatrix} X \\ Y \\ Z \end{pmatrix}=\begin{pmatrix} 2.7688 & 1.7517 & 1.1301 \\ 1.0000 & 4.5906 & 0.060067 \\ 0.0000 & 0.056507 & 5.5942 \end{pmatrix}\begin{pmatrix} R_{\mathrm{CIE}} \\ G_{\mathrm{CIE}} \\ B_{\mathrm{CIE}} \end{pmatrix}\tag{1}$$コードで導入
自分で下記コードを<head>~</head>内に記載します。
こうすることで、いちいちショートコードで指定などが必要なくなります。でも、全ページでMathJaxが読み込まれるので、少々重くはなると思います。
シンプル導入
参考サイト: https://www.mathjax.org/#gettingstarted
<script id="MathJax-script" async src="https://cdn.jsdelivr.net/npm/mathjax@3.2.2/es5/tex-mml-chtml.js"></script>こうすることで、インラインでは \( ...数式... \) とすることで、数式行では \[ ...数式... \] とすることで実現ができます。
2次方程式 \(ax^2 + bx + c = 0\) の解の公式は、 \(a \ne 0\)のとき、
\[x = {-b \pm \sqrt{b^2-4ac} \over 2a}\]
となる。2次方程式 \(ax^2 + bx + c = 0\) の解の公式は、 \(a \ne 0\)のとき、
\[x = {-b \pm \sqrt{b^2-4ac} \over 2a}\]
となる。
カスタム
下記サイトを参考に、インライン数式をドルで挟む記法($ ...数式... $)を使えるように拡張します。下記コードをhead内に記入。
<script>
MathJax = {
tex: {
inlineMath: [['$', '$'], ['\\(', '\\)']]
}
};
</script>
<script id="MathJax-script" async src="https://cdn.jsdelivr.net/npm/mathjax@3.2.2/es5/tex-mml-chtml.js"></script>2次方程式 $ax^2 + bx + c = 0$ の解の公式は、 $a \ne 0$のとき、
\[x = {-b \pm \sqrt{b^2-4ac} \over 2a}\]
となる。参考サイト: https://easy-copy-mathjax.nakaken88.com/introduction
CSSカスタム
長い数式をスマホで表示すると、横にはみ出してしまうことがあります。それを阻止するためのCSSです。
スタイルシートStylesheet (style.css)内に記入してください。もしくは、<style type="text/css"></style>タグの中に入れます。
/* ディスプレイ数式用の mjx-container をブロック&横スクロール可に */
mjx-container[jax="CHTML"][display="true"] {
display: block !important; /* ブロック要素として扱う */
position: relative !important; /* 絶対配置の子要素(mjx-labels)を枠内に留める */
max-width: 100% !important; /* 親要素の横幅を超えない */
overflow-x: auto !important; /* 横スクロールを有効にする */
overflow-y: hidden !important; /* 不要なら縦スクロールは非表示に */
/* MathJax が算出する余計な min-width を打ち消す */
min-width: auto !important;
}
/* 数式タグ(式番号)を container 内に絶対配置する */
mjx-container[jax="CHTML"][display="true"] mjx-labels {
position: absolute !important; /* 枠の中に固定 */
right: 0.5em !important; /* 好みで調整。タグを右端に寄せる */
top: 0.2em !important; /* 好みで上揃えを少し下げる */
width: auto !important;
min-width: 0 !important;
}
参考サイトや、AIに頼って作成しました。ポイントは、MathJax v2とv3でいろいろ変わっていること(v2は、spanタグ内に数式があったが、v3から、mjx-containerというタグの中に数式がある)、式番号があるとどうしてもはみ出がちになっちゃうというところです。
参考サイト:https://sj-note.com/mathjax-scroll
参考サイト:https://stackoverflow.com/questions/65321568/mathjax-3-inline-math-and-overflow-x
参考サイト:https://stackoverflow.com/questions/65264328/mathjax-3-change-css-styles
参考サイト(これはv2の書き方):https://uni-files.com/mathjax-latex-wordpress-%E6%95%B0%E5%BC%8F%E3%81%8C%E3%81%AF%E3%81%BF%E5%87%BA%E3%82%8B%E5%95%8F%E9%A1%8C%E3%81%AE%E8%A7%A3%E6%B1%BA%E7%AD%96/
MathJaxのデメリット
ほとんどのウェブサイトで採用されているということで、ほぼデメリットはありません。唯一挙げられるのが、少々重いということ。
KaTeX
MathJaxより軽量な数式表示JavaScriptライブラリに、「KaTeX」というものがあります。これは厳密にはLaTeXではないらしいのですが、LaTex互換です。ほとんどの数式に対応しているようで、たいていのことができます。有名サイトでは、ブログ記事サイトnoteで数式記入の仕組みに採用されてます。
noteの記事:https://note.com/info/n/n8d5153b3a136
参考サイト1:https://zenn.dev/papanyanko/articles/non-phper-enhancing-wp-plugin-with-claude
参考サイト2:https://www.kennzo.net/wordpress-latex
参考サイト3:https://katex.org/docs/autorender
コードで導入
KaTeXは、WordPressプラグインで簡単投入する方法は現在ではないようです。どうやらKaTeXプラグインは存在するにはするんですが、かなり古い。まあべつにプラグイン入れるまでもないので、直接コードを書きます。
私は、参考サイトの人とおなじように、Cocoonというテーマを使ってます。なので、Cocoon Child: head-insert.php (tmp-user/head-insert.php)に下記コードを挿入。
メニュー→外観→テーマファイルエディター→Cocoon Child→tmp-user/head-insert.php
<link rel="stylesheet" href="https://cdn.jsdelivr.net/npm/katex@0.16.15/dist/katex.min.css" integrity="sha384-Htz9HMhiwV8GuQ28Xr9pEs1B4qJiYu/nYLLwlDklR53QibDfmQzi7rYxXhMH/5/u" crossorigin="anonymous">
<!-- The loading of KaTeX is deferred to speed up page rendering -->
<script defer src="https://cdn.jsdelivr.net/npm/katex@0.16.15/dist/katex.min.js" integrity="sha384-bxmi2jLGCvnsEqMuYLKE/KsVCxV3PqmKeK6Y6+lmNXBry6+luFkEOsmp5vD9I/7+" crossorigin="anonymous"></script>
<!-- To automatically render math in text elements, include the auto-render extension: -->
<script defer src="https://cdn.jsdelivr.net/npm/katex@0.16.15/dist/contrib/auto-render.min.js" integrity="sha384-hCXGrW6PitJEwbkoStFjeJxv+fSOOQKOPbJxSfM6G5sWZjAyWhXiTIIAmQqnlLlh" crossorigin="anonymous"
onload="renderMathInElement(document.body);"></script>コードは、KaTeX公式サイト(参考サイト3)からコピペです。
これで、
$$x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$$のようにドルドルで挟むか、
\[x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\]のようにエスケープ角カッコで数式になります。
インライン数式にしたければ
数式\(x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\)です。のように、エスケープ丸カッコで書けます。
ちなみに、複数行にわたる場合は、エスケープを2回書かないといけません。あと、コードが複数行になるとうまくいかない?ので一行で書くようにしましょう。
KaTeXのデメリット
表現の幅が狭かったり、Web上の情報が少なかったりですかね。ということでこのサイトではMathJaxを使うことにしました。
数式例
現状、このサイトはMathJaxを採用しています。
WordPressで数式 \(x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\) を書きたい!WordPressで数式 \(x = \frac{-b \pm \sqrt{b^2 – 4ac}}{2a}\) を書きたい!
$$x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$$$$x = \frac{-b \pm \sqrt{b^2 – 4ac}}{2a}$$
\[\sin^2 \theta + \cos^2 \theta = 1\]\[\sin^2 \theta + \cos^2 \theta = 1\]
$$\mathbf{A} = \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{bmatrix}$$$$\mathbf{A} = \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{bmatrix}$$
$$\begin{pmatrix} X \\ Y \\ Z \end{pmatrix}=\begin{pmatrix} 2.7688 & 1.7517 & 1.1301 \\ 1.0000 & 4.5906 & 0.060067 \\ 0.0000 & 0.056507 & 5.5942 \end{pmatrix}\begin{pmatrix} R_{\mathrm{CIE}} \\ G_{\mathrm{CIE}} \\ B_{\mathrm{CIE}} \end{pmatrix}\tag{1}$$
$$\begin{pmatrix} R_{\mathrm{CIE}} \\ G_{\mathrm{CIE}} \\ B _{\mathrm{CIE}}\end{pmatrix}=\begin{pmatrix} 0.41847 & -0.15866 & -0.082835 \\ -0.091169 & 0.25243 & 0.015708 \\ 0.00092090 & -0.0025498 & 0.17860 \end{pmatrix}\begin{pmatrix} X \\ Y \\ Z \end{pmatrix}\tag{2}$$
$$\begin{pmatrix} X \\ Y \\ Z \end{pmatrix}=\begin{pmatrix} 0.412453 & 0.357580 & 0.180423 \\ 0.212671 & 0.715160 & 0.072169 \\ 0.019334 & 0.119193 & 0.950277 \end{pmatrix}\begin{pmatrix} R_{709} \\ G_{709} \\ B_{709} \end{pmatrix}\tag{3}$$
$$\begin{pmatrix} R_{709} \\ G_{709} \\ B_{709} \end{pmatrix}=\begin{pmatrix} 3.240479 & -1.537150 & -0.498535 \\ -0.969256 & 1.875992 & 0.041556 \\ 0.055648 & -0.204043 & 1.057311 \end{pmatrix}\begin{pmatrix} X \\ Y \\ Z \end{pmatrix}\tag{4}$$$$\begin{pmatrix} X \\ Y \\ Z \end{pmatrix}=\begin{pmatrix} 2.7688 & 1.7517 & 1.1301 \\ 1.0000 & 4.5906 & 0.060067 \\ 0.0000 & 0.056507 & 5.5942 \end{pmatrix}\begin{pmatrix} R_{\mathrm{CIE}} \\ G_{\mathrm{CIE}} \\ B_{\mathrm{CIE}} \end{pmatrix}\tag{1}$$
$$\begin{pmatrix} R_{\mathrm{CIE}} \\ G_{\mathrm{CIE}} \\ B _{\mathrm{CIE}}\end{pmatrix}=\begin{pmatrix} 0.41847 & -0.15866 & -0.082835 \\ -0.091169 & 0.25243 & 0.015708 \\ 0.00092090 & -0.0025498 & 0.17860 \end{pmatrix}\begin{pmatrix} X \\ Y \\ Z \end{pmatrix}\tag{2}$$
$$\begin{pmatrix} X \\ Y \\ Z \end{pmatrix}=\begin{pmatrix} 0.412453 & 0.357580 & 0.180423 \\ 0.212671 & 0.715160 & 0.072169 \\ 0.019334 & 0.119193 & 0.950277 \end{pmatrix}\begin{pmatrix} R_{709} \\ G_{709} \\ B_{709} \end{pmatrix}\tag{3}$$
$$\begin{pmatrix} R_{709} \\ G_{709} \\ B_{709} \end{pmatrix}=\begin{pmatrix} 3.240479 & -1.537150 & -0.498535 \\ -0.969256 & 1.875992 & 0.041556 \\ 0.055648 & -0.204043 & 1.057311 \end{pmatrix}\begin{pmatrix} X \\ Y \\ Z \end{pmatrix}\tag{4}$$
\[\begin{pmatrix} X \\ Y \\ Z \end{pmatrix}=\begin{pmatrix} 2.7688 & 1.7517 & 1.1301 \\ 1.0000 & 4.5906 & 0.060067 \\ 0.0000 & 0.056507 & 5.5942 \end{pmatrix}\begin{pmatrix} R_{\mathrm{CIE}} \\ G_{\mathrm{CIE}} \\ B_{\mathrm{CIE}} \end{pmatrix}\]\[\begin{pmatrix} X \\ Y \\ Z \end{pmatrix}=\begin{pmatrix} 2.7688 & 1.7517 & 1.1301 \\ 1.0000 & 4.5906 & 0.060067 \\ 0.0000 & 0.056507 & 5.5942 \end{pmatrix}\begin{pmatrix} R_{\mathrm{CIE}} \\ G_{\mathrm{CIE}} \\ B_{\mathrm{CIE}} \end{pmatrix}\]
\[\lim_{x \to 0} (1+x)^{\frac{1}{x}} = e \]\[\lim_{x \to 0} (1+x)^{\frac{1}{x}} = e \]
$$\mathbf{a} \cdot \mathbf{b} = |\mathbf{a}| |\mathbf{b}| \cos \theta$$$$\mathbf{a} \cdot \mathbf{b} = |\mathbf{a}| |\mathbf{b}| \cos \theta$$
$$P(A \cap B) = P(A)P(B)$$$$P(A \cap B) = P(A)P(B)$$
\[\frac{\mathrm{d}y}{\mathrm{d}x} = 3x^2 + 2x + 1\]\[\frac{\mathrm{d}y}{\mathrm{d}x} = 3x^2 + 2x + 1\]
\[\int_0^1 x^2 \, \mathrm{d}x = \frac{1}{3}\]\[\int_0^1 x^2 \, \mathrm{d}x = \frac{1}{3}\]
$$\ket{\Psi} = \ket{\mathbf{r}} \otimes \ket{\uparrow} \quad \text{or} \quad \ket{\Psi} = \ket{\mathbf{r}} \otimes \ket{\downarrow}$$$$\ket{\Psi} = \ket{\mathbf{r}} \otimes \ket{\uparrow} \quad \text{or} \quad \ket{\Psi} = \ket{\mathbf{r}} \otimes \ket{\downarrow}$$
\[ c = \pm\sqrt{a^2 + b^2} \]\[ c = \pm\sqrt{a^2 + b^2} \]
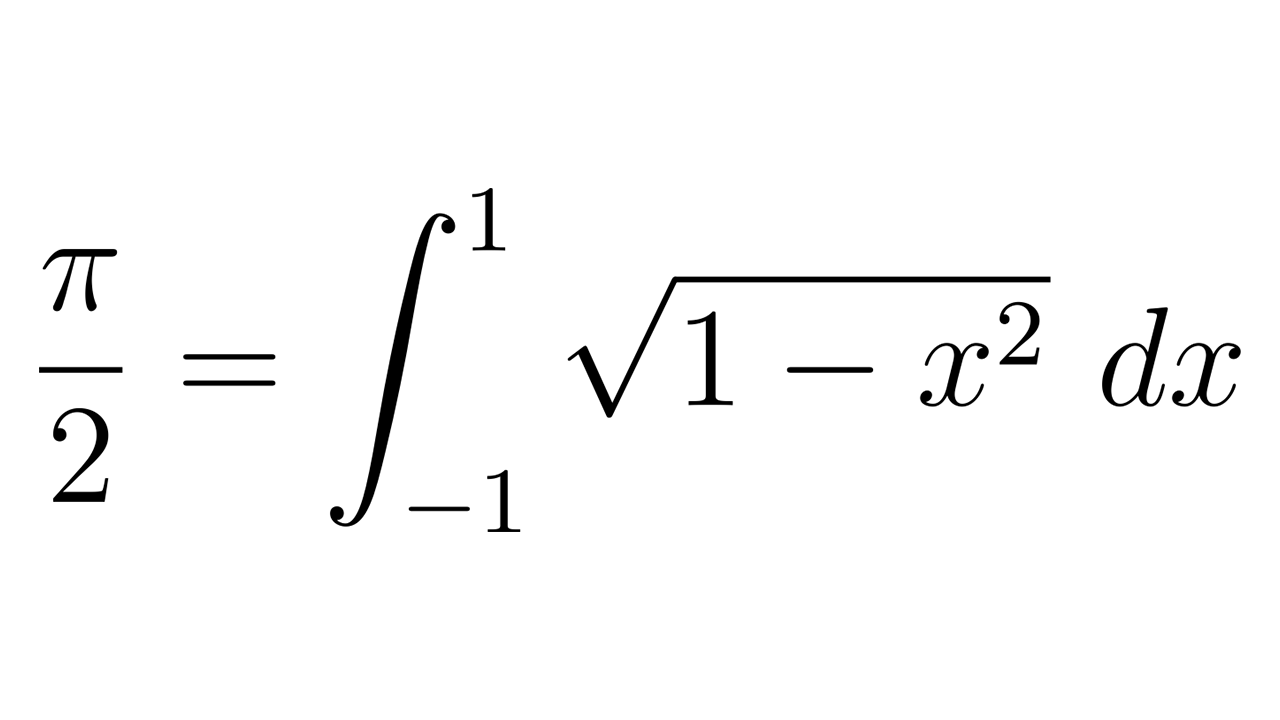


コメント